Phần 7: Cấu trúc sóng điều chỉnh và Mối quan hệ Fibonacci trong Sóng Elliott

Hiểu về các điều chỉnh hình tam giác

Tam giác là các mô hình điều chỉnh di chuyển ngang chứ không theo xu hướng. Chúng phân chia thành năm sóng, được dán nhãn A–B–C–D–E, và thường phản ánh một sự tạm dừng trước giai đoạn cuối cùng của một động thái lớn hơn.

Cấu trúc bên trong của chúng hầu như luôn luôn là điều chỉnh, tạo thành một mô hình 3–3–3–3–3. Điều này phân biệt tam giác với các hình thành xung động.

Tam giác thường xuất hiện nhất:

• Như sóng 4 trong một xung động

• Như sóng B trong một điều chỉnh lớn hơn

• Là cấu trúc cuối cùng trong một điều chỉnh phức tạp

Chúng không xuất hiện như một sóng 2 độc lập.

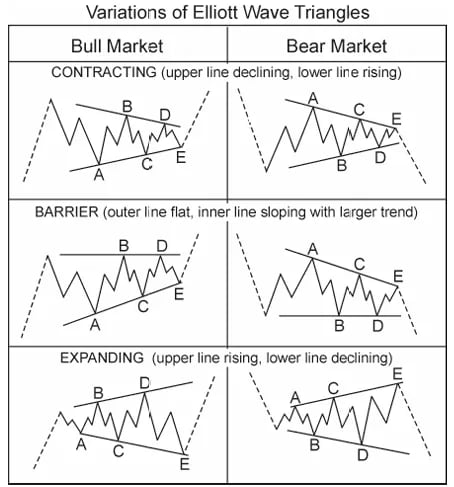
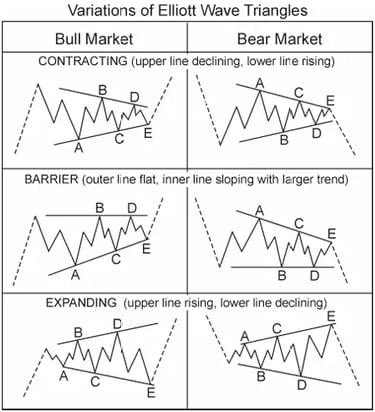
Biến thể của tam giác

Tam giác hình thành trong một số biến thể, mỗi biến thể được xác định bởi hành vi của các ranh giới của nó.

• Tam giác thu hẹp (phổ biến nhất) dần thu hẹp khi mỗi sóng trở nên nhỏ hơn

• Tam giác Barrier duy trì một ranh giới ngang trong khi phía đối diện thu hẹp

• Tam giác mở rộng (hiếm) mở rộng theo thời gian và tương đối hiếm

Bất kể loại, mục đích của chúng là giống nhau: củng cố trước khi giải quyết.

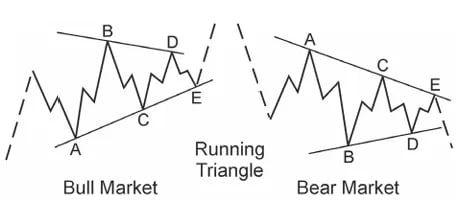
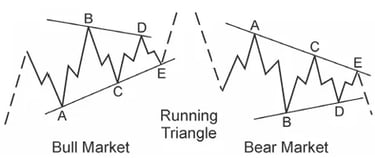
Tam giác Chạy và Sức mạnh Xu hướng

Khi sóng B đẩy vượt quá nguồn gốc của Sóng A, tam giác trở nên “chạy.” Biến thể này thường báo hiệu áp lực xu hướng cơ bản mạnh.

Thay vì làm suy yếu xu hướng, một tam giác chạy cho thấy thị trường đang nén năng lượng trước khi tiếp tục. Những hình thành này thường đi trước các động thái định hướng sắc nét.

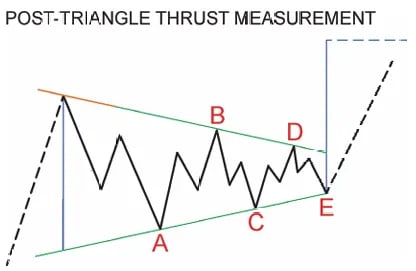
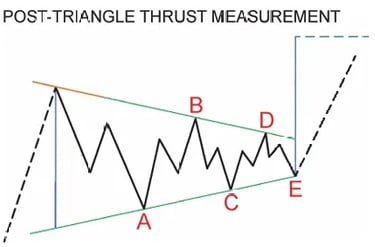
Đẩy sau Tam giác

Tam giác rất có giá trị vì chúng thường đi trước sóng động lực cuối cùng của một chuỗi. Khi tam giác được giải quyết, giá thường tăng tốc nhanh chóng. Phép đo lực đẩy sau tam giác cung cấp một cách đáng tin cậy để đo lường mức độ di chuyển của giá sau khi xảy ra đột phá tam giác.

Cách đo lực đẩy:

1. Vẽ đường xu hướng kết nối sóng A-C và B-D

2. Kéo dài các đường này trở lại điểm bắt đầu của sóng A

3. Đo khoảng cách dọc giữa các đường xu hướng ("chiều rộng" của tam giác)

4. Áp dụng chiều rộng này từ điểm cuối của sóng E để ước tính mục tiêu lực đẩy tối thiểu

   Nếu bạn xác định được một tam giác, hãy mong đợi một sóng động lực nữa sẽ theo sau - tam giác luôn đi trước bước di chuyển cuối cùng.

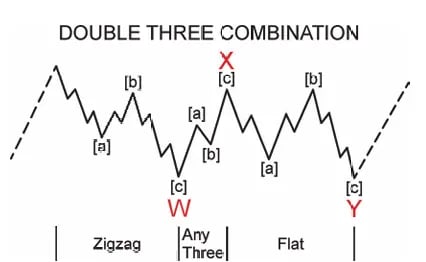
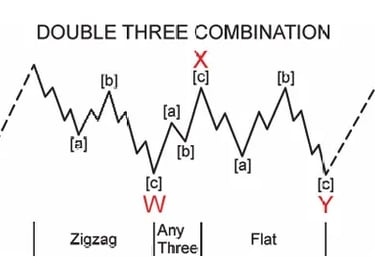
Sửa đổi phức tạp và Kết hợp

Không phải tất cả các điều chỉnh đều diễn ra rõ ràng. Khi thị trường cần nhiều thời gian hơn hoặc cần điều chỉnh sâu hơn, chúng có thể liên kết nhiều cấu trúc điều chỉnh lại với nhau. Những hình thái này được gọi là kết hợp.

Các kết hợp:

• Bao gồm hai hoặc nhiều cấu trúc điều chỉnh (giới hạn dường như là ba)

• Mỗi cấu trúc được liên kết bởi một sóng X di chuyển ngược lại với mô hình trước đó

• Sóng X thường là zigzag (và có thể có vẻ ngoài xung động) nhưng chúng có thể là bất kỳ mô hình điều chỉnh nào ngoại trừ tam giác

• Chỉ một tam giác có thể xuất hiện trong một kết hợp, và nó luôn là cấu trúc cuối cùng

• Sự kết hợp WXY cũng thể hiện dấu hiệu xen kẽ, ví dụ, nếu sóng W là một sự điều chỉnh ngang (sửa chữa ngang), sóng Y thường sẽ xen kẽ như một zigzag (sửa chữa sắc nét) và ngược lại. Sự xen kẽ này giúp xác định và phân biệt các cấu trúc điều chỉnh nội bộ.

Chỉ một tam giác có thể xuất hiện trong một sự kết hợp, và nó luôn xảy ra ở cuối.

Mặc dù gây khó khăn khi giao dịch nội bộ, các sự kết hợp thường dẫn đến những bước đi quyết đoán một khi hoàn thành.

Mối quan hệ Fibonacci như là Xác thực Cấu trúc

Tỷ lệ Fibonacci cung cấp ngữ cảnh tỷ lệ trong Sóng Elliott. Thay vì dự đoán chính xác điểm quay đầu, chúng giúp xác định liệu một cấu trúc có còn phù hợp với hướng dẫn của nó hay không.

Trong sóng xung lực:

• Sóng 2 thường thoái lui khoảng 61,8% của sóng 1 (điều chỉnh sâu)

• Sóng 4 thường thoái lui khoảng 38,2% của sóng 3 (điều chỉnh nông)

Sự xen kẽ giữa các điều chỉnh sâu và nông là một trong những hướng dẫn đáng tin cậy nhất của Sóng Elliott. Vì vậy, nếu sóng 2 sâu, hãy tìm sóng 4 nông và ngược lại.

Những tỷ lệ này giúp các nhà giao dịch đánh giá liệu một sóng đang phát triển có hoạt động bình thường hay trở nên đáng ngờ về mặt cấu trúc.

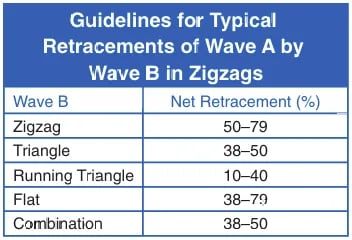
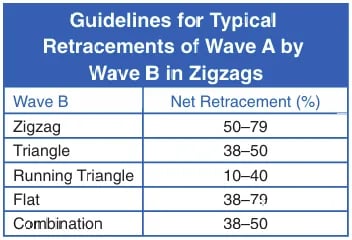
Trong các điều chỉnh zigzag, mức thoái lui của sóng B so với sóng A phụ thuộc vào cấu trúc bên trong của B:

• Nếu sóng B là zigzag: 50-78,6% thoái lui

• Nếu sóng B là tam giác: 38,2-50% thoái lui

• Nếu sóng B là phẳng: 38,2-78,6% thoái lui

Hành vi thoái lui trong Sóng điều chỉnh

Các cấu trúc điều chỉnh khác nhau thể hiện các xu hướng thoái lui khác nhau.

• Các điều chỉnh sắc nét thường thoái lui sâu

• Các điều chỉnh ngang có xu hướng thoái lui ít hơn về giá nhưng tiêu tốn nhiều thời gian hơn

• Sự xen kẽ giữa các hành vi này là một hướng dẫn tái diễn

Hiểu được những xu hướng này giúp duy trì kỳ vọng thực tế trong quá trình củng cố.

Tỷ lệ và sự bằng nhau của độ dài sóng

Trong cả sóng xung lực và sóng điều chỉnh, các mối quan hệ tỷ lệ thường xuyên lặp lại.

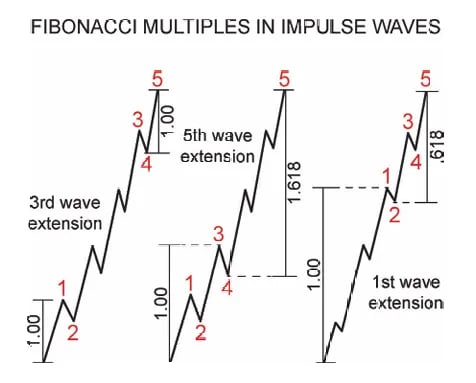
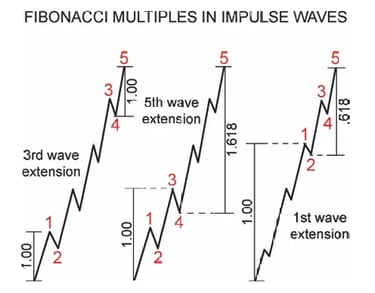
Đối với sóng xung lực:

• Khi sóng 3 mở rộng, sóng 5 thường bằng sóng 1 hoặc 61,8% của sóng 1

• Khi sóng 5 mở rộng, nó thường di chuyển 161,8% của tổng sóng 1-3

• Khi sóng 1 mở rộng, tổng sóng 3-5 thường bằng 61,8% của sóng 1

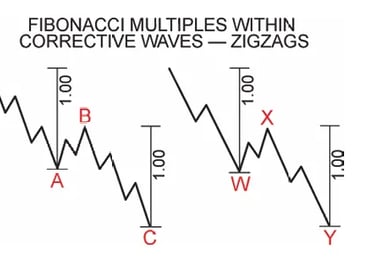
Đối với các điều chỉnh zigzag:

• Mối quan hệ phổ biến nhất: Sóng C bằng sóng A (sự bằng nhau)

• Mối quan hệ thay thế: C = 61,8% của A, hoặc C = 161,8% của A

• Trong zigzag kép: Sóng Y thường bằng sóng W

Những mối quan hệ này giúp các nhà giao dịch tránh ép buộc các diễn giải không phù hợp với tỷ lệ quan sát được.

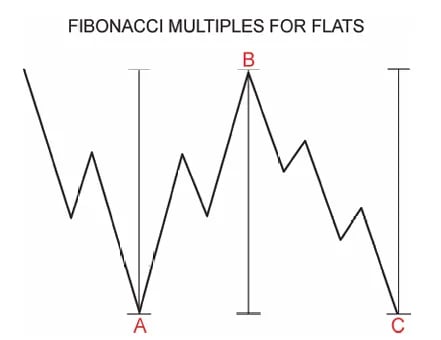
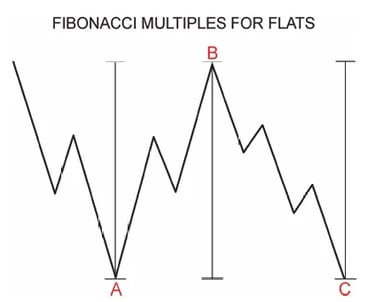
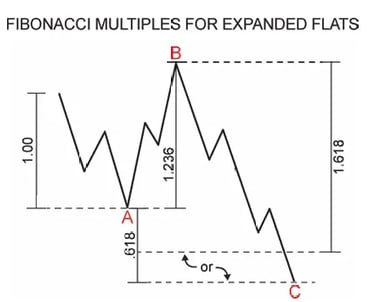
Mối quan hệ Fibonacci trong điều chỉnh phẳng

Đáy phẳng thông thường: Sóng A, B, và C thường có độ dài bằng nhau

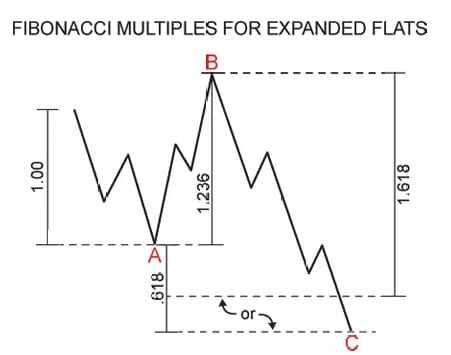
Đáy phẳng mở rộng (phức tạp hơn nhưng phổ biến hơn):

• Sóng C = 161,8% của sóng A, hoặc

• Sóng C kết thúc 61,8% của sóng A vượt quá điểm cuối của sóng A

• Sóng B = 123,6% hoặc 138,2% của sóng A

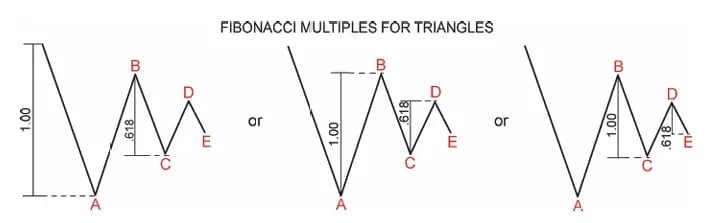
Hiệu chỉnh tam giác co lại của các mối quan hệ Fibonacci

• Sóng C = 61,8% của sóng B

• Sóng D = 61,8% của sóng C

• Sóng E = 61,8% của sóng D. Những mối quan hệ này giúp xác thực cấu trúc tam giác và xác định các điểm kết thúc có thể xảy ra cho mỗi chân sóng.

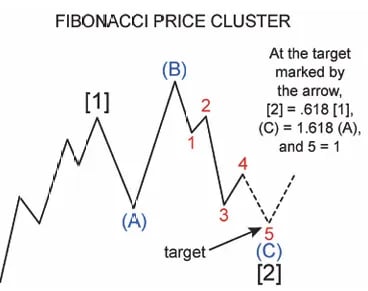
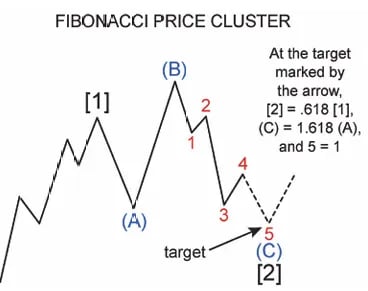
Cụm Fibonacci và Vùng có xác suất cao

Thông tin chi tiết hữu ích nhất của Fibonacci không đến từ một tỷ lệ đơn lẻ, mà từ sự hội tụ.

Cụm Fibonacci hình thành khi nhiều phép đo độc lập cùng chỉ đến một vùng giá nhất định. Những vùng này thường hoạt động như:

• Điểm kết thúc điều chỉnh

• Mục tiêu mở rộng

• Mức phản ứng quan trọng

Cụm Fibonacci củng cố niềm tin bằng cách liên kết cấu trúc với tỷ lệ, khi 2 hoặc nhiều mối quan hệ Fibonacci đồng nhất, xác suất điểm quay đầu của thị trường tăng lên đáng kể.

Bài học này phù hợp với chuỗi như thế nào

Bài học này cung cấp nền tảng cấu trúc và tỷ lệ để thực hiện phân tích Sóng Elliott trong giai đoạn điều chỉnh. Nó giải thích lý do tại sao sự kiên nhẫn thường được yêu cầu và làm thế nào sự rõ ràng vẫn có thể được duy trì khi giá dường như không có hướng.

Bài học tiếp theo tập trung vào thực thi, chuyển sự hiểu biết cấu trúc này thành các quyết định giao dịch dựa trên xác nhận tôn trọng sự không chắc chắn.

Chuỗi Khóa học Giao dịch Sóng Elliott

Bài viết này là một phần của Khóa học Giao dịch Sóng Elliott .

Các bài học trong chuỗi này:

• Phần 1: Tại sao Sóng Elliott Thất bại với Hầu hết Các Nhà giao dịch

• Phần 2: Cấu trúc Thị trường Đơn giản Giải thích Mọi Sự Biến động Giá

• Phần 3: Tại sao Sóng Elliott Cung cấp Nhiều Ngữ cảnh Hơn Các Chỉ số Truyền thống

• Phần 4: Các Pha Sóng Elliott Mang lại Cơ hội Giao dịch Rõ ràng Nhất

• Phần 5: Phần mở rộng và Cắt ngắn Sóng Elliott

• Phần 6: Sóng Chéo và Các Mẫu Điều chỉnh

• Phần 7: Cấu trúc sóng điều chỉnh và Mối quan hệ Fibonacci trong Sóng Elliott

• Phần 8: Áp dụng Cấu trúc Sóng Elliott với Việc Thực hiện Giao dịch Dựa trên Xác nhận

• Phần 9: Quản lý Rủi ro và Tâm lý

• Phần 10: Khung giao dịch Sóng Elliott Hoàn chỉnh